Pubblichiamo oggi il bellissimo post tecnico di Alberto Bagnai tratto dal suo blog http://goofynomics.blogspot.it che spiega con gran classe come tornando alla nostra moneta sovrana l'aumento dei prezzi delle materie prime non ci deve spaventare ma anzi abbiamo le carte per essere i migliori e ritornare nella posizione economica che ci spetta e che questo aborto di Euro ci ha portato via.
Buona lettura e astenersi piddini....
(post tecnico)
Una doverosa precisazione terminologica
Visto che la famiglia cresce e che gli ultimi arrivati rigorosamente non si conformano al precetto di consultare le istruzioni per l’uso, mi corre l’obbligo di premettere una breve nota terminologica che permetta comunque loro di raccapezzarsi nella complessa commedia (o forse tragedia) umana che questo blog va rappresentando da un anno. Particolarmente importante in tal senso è la distinzione fra piddino, PDno e PUDino. In sintesi:
1) il piddino è qualsiasi essere umano dotato di un unico neurone;
2) il PDno è un iscritto/simpatizzante/elettore del PD;
3) il PUDino è un iscritto/simpatizzante/elettore del PUDE, partito unico dell’euro.
La terza categoria è la più ampia. Ad oggi, chiunque voti voterà PUDE (qualsiasi cosa voti). Non esistono, ad oggi, sufficienti prove del contrario, cioè del fatto che si possa votare “non PUDE”. Non fatemi esempi del belìno (termine scelto non a caso) perché non ci voglio perder tempo qui. Se son rose fioriranno e ne sarò lietissimo (festeggeremo così il mio primo errore), ma una rondine non fa primavera.
La seconda categoria è la più facile da definire, e quindi non ci spendo molte parole.
La prima categoria, quella del piddino, è la più difficile da individuare per chi non ha seguito lo sforzo di approfondimento che abbiamo condotto in questo blog. Il piddino ha un unico neurone, dicevamo, che dedica notoriamente a un unico compito: il sapere di sapere. Il piddino sa di sapere: di questa stravagante e perniciosa filosofia abbiamo parlato a lungo. Capisco che qualche PDno possa essere incuriosito dall’etimologia del termine “piddino”. Gli suggerisco di non indagare troppo.
Volete esempi: Monti è PUDino, ma ovviamente non PDno e certo non piddino. Fassina è certamente PDno, quindi ovviamente PUDino, ma forse non piddino. La ‘zdora racchiude in se tutte e tre queste categorie. Ingroia, Ferrero, ecc. sono tutti PUDini, anche se non sono PDni... e qui mi fermo. Vogliamo dire una parola buona anche a Crosetto? So che non è piddino, e tutti vedono che non è nemmeno PDno: quindi, come Monti, è solo PUDino (non gli farà piacere essere in questa compagnia, ma se l’è scelta da solo)!
Il motivo per il quale invito i piddini ad astenersi dal leggere questo post è che purtroppo per farlo occorrono tre neuroni: quindi, piddino caro, o ti fai prestare i due che ti mancano...
Propensione ed elasticità
Supponiamo che una variabile y dipenda da una variabile x. Esempio: il consumo dipende dal reddito. I matematici indicano questa dipendenza così: y = f(x), che si legge: “y è funzione di x”, cioè varia in funzione di come varia x.
Di questa dipendenza in genere ci interessano due cose: il segno, e l’intensità.
Nel caso “reddito-consumo” il segno è certamente positivo: se guadagni di più, spendi di più. Nel caso “prezzo-domanda di un bene” la relazione è normalmente negativa: se un bene costa di più, normalmente ne chiedi di meno, cerchi di sostituirlo con un bene che
costa di meno. Questo per quanto riguarda il segno, che può quindi essere positivo o negativo.
costa di meno. Questo per quanto riguarda il segno, che può quindi essere positivo o negativo.
Per quanto riguarda l’intensità, in macroeconomia ci sono due modi di misurarla.
Il primo è la propensione marginale, che è definita come il rapporto fra le due variazioni. Supponiamo che quando il reddito aumenta di 10, i consumi aumentino di 7. La propensione marginale è:
Una propensione marginale al consumo di 0.7 indica che il 70% di ogni incremento di reddito viene indirizzato a nuovi consumi. Evidentemente, in questo caso la propensione marginale al risparmio sarà del 30% (quello che non viene consumato viene risparmiato).
Il secondo è l’elasticità, definita come rapporto fra due variazioni percentuali. Per definirla dobbiamo conoscere non solo di quanto variano x e y, ma anche qual è il loro valore iniziale (prima della variazione), altrimenti non siamo in grado di esprimere le variazioni in termini percentuali.
Ad esempio, se, nel caso precedente, il livello iniziale del consumo è 50 e quello del reddito è 100, l’elasticità sarà:
che poi significa che in quel punto, la variazione percentuale del consumo è il 140% di quella del reddito (il reddito aumenta del 10%, il consumo del 140%).
Nota bene: in questo caso il rapporto fra le due variabili, cioè la propensione media, aumenta, perché il numeratore (y) in proporzione è aumentato più del denominatore (x). Infatti, prima della variazione il rapporto è 50/100=0.5=50%, dopo la variazione il rapporto è 57/110=0.51818=52%.
Se invece il livello iniziale del consumo fosse 80, lasciando invariato tutto il resto, l’elasticità sarebbe:
cioè: solo l’87.5% dell’incremento percentuale di reddito si trasforma in un incremento percentuale del consumo. Ovviamente in questo caso, visto che il numeratore varia proporzionalmente di meno, il rapporto diminuisce (verificare per credere).
L’elasticità è un concetto relativamente più complesso, ma molto utile, perché in economia spesso ci interessa sapere in quale proporzione reciproca si vengono a trovare certi effetti. Insomma: le variazioni percentuali sono più significative di quelle assolute, e quindi, purtroppo, le elasticità ci danno informazioni più utili delle propensioni marginali.
Il caso più ovvio è quello nel quale ci interessa sapere se due variabili evolvono mantenendo un rapporto costante (cioè una propensione media costante). Questa caratteristica, definita crescita bilanciata, è molto importante nell’analisi dinamica, perché definisce alcuni stati stazionari, cioè situazioni di equilibrio di lungo periodo. Vi immaginate, ad esempio, che non è concepibile una situazione di lungo periodo nella quale il rapporto consumo/reddito non si stabilizzi: se diminuisse per sempre, il consumatore morrebbe di fame; se aumentasse per sempre, il consumatore esploderebbe. Quindi normalmente il lungo periodo è caratterizzato da crescita bilanciata. Ma la crescita bilanciata richiede che l’elasticità fra le due variabili considerate sia uguale a uno, cioè che numeratore e denominatore crescano nella stessa proporzione (stessa variazione percentuale): solo così il loro rapporto può restare costante.
L’incubo del materieprimista
Dal meraviglioso mondo dei dilettanti dell’economia ci giungono fantasiose ipotesi su cosa accadrebbe se l’Italia riacquistasse la propria sovranità valutaria e monetaria. Qui ci occupiamo della prima, cioè del fatto di emettere un valuta nazionale liberamente commerciata sui mercati dei cambi (e quindi soggetta a fluttuazione). Sì, proprio quella cosa che gli spaghetti-liberisti aborrono, mentre, chissà perché, i veri liberisti, come Milton Friedman, quelli che credono in tutti i mercati, compreso quello dei cambi, ovviamente ritengono fisiologica e desiderabile.
Quei dilettanti particolarmente fastidiosi e patetici che sono i materieprimisti (definizione di Claudio Borghi Aquilini) insistono sul fatto che siccome è noto che l’Italia svaluterebbe (per recuperare il differenziale di inflazione cumulato con la Germania), ciò aggraverebbe irrimediabilmente il nostro deficit, perché dovremmo pagare proporzionalmente di più le materie prime...
Poveri materieprimisti! Li ho sempre presi in giro, ma questa sera mi sono accorto che in effetti hanno ragione loro. Mi scuso quindi con loro: è vero, compatibilmente con la struttura del loro cervello mononeuronale, effettivamente andremmo in deficit. Vi spiego perché.
Supponiamo che la bilancia commerciale parta da una posizione di equilibrio. Potremmo esprimere questo equilibrio così:
PX = EPfM
dove P sono i prezzi nazionali, X le esportazioni, E il tasso di cambio incerto per certo (quantità di valuta nazionale per una unità di valuta estera), Pf i prezzi esteri in valuta estera, M le importazioni. La condizione qua sopra ci dice che il valore delle esportazioni (prezzo dei beni per quantità) uguaglia quello delle importazioni (che siccome sono prezzate in valuta estera, devono essere convertite in valuta nazionale col cambio). Ora, nel caso considerato, una svalutazione corrisponde a un aumento di E. Chi ha un neurone solo ovviamente vede solo quello, e quindi giustamente nota che se E aumenta, a parità di altri condizioni (col vostro riverito permesso dirò ceteris paribus, una clausola della quale abbiamo bisogno dato che i piddini sono endemici), il valore delle importazioni (quello che dobbiamo pagare per averle) aumenta, e quindi andiamo in rosso.
Orrore!
A questo punto il materieprimista rinfodera l’unico neurone che possiede e si allontana soddisfatto: è convinto di averci asfaltato, e a noi piace ricordarlo così, appagato da questa sua beota convinzione. Lasciamolo andare: se non lui, il suo modo di ragionare emana un fetore del quale siamo lieti di liberarci il prima possibile. Non fate l’errore di tentare di convincerlo: il ragionamento tecnico non riesce a seguirlo (ne saranno prova le domande a questo post), e i precedenti storici non lo convinceranno mai, perché il materieprimista strutturalmente appartiene alla categoria dei fuuuuuuuuuuuuuuurbi: sì, quelli che confutano le strampalate teorie di Bagnai, quelli che si sono formati in economia leggendo assiduamente gli inserti di Repubblica. I fuuuuuuuuuuuuuurbi sono una miniera sterminata di aneddoti: dei bulimici collezionisti di foglie, che usano a mo’ di lenti a contatto per non rischiare di vedere l’albero. Prepariamo la borsa del ghiaccio per l’inevitabile bernoccolo e andiamo avanti, ma non prima di aver fatto un opportuno “disegnino” con lo scenario del materieprimista:
L’ho tenuto semplice: i prezzi e il cambio nella baseline (lo scenario di partenza) sono tutti normalizzati a uno, e i volumi scambiati sono identici e uguali a 50. In questo caso il valore delle esportazioni e delle importazioni coincidono e sono uguali anche loro a 50, e il saldo commerciale è nullo. Ci siete?
Il materieprimista vede solo l’aumento del cambio determinato dalla svalutazione. Nel caso in specie, ho immaginato una svalutazione del 20% (cioè: il cambio passa a 1.2, occorre il 20% in più di valuta nazionale per acquistare la valuta estera), quindi il valore delle esportazioni resta invariato a PxX=1x50=50, quello delle importazioni passa da 1x1x50=50 a 1.2x1x50=60 e quindi il saldo passa a 50-60=-10.
Deficit! Sciagura! Criminali insensati, ecco dove ci ha portato il vostro folle volo! Perché avete abbandonato l’euro che ci protegge...
La condizione di Marshall-Lerner
Il problema è che solo un perfetto cretino può immaginare una simile clausola ceteris paribus. In realtà sappiamo benissimo, perché lo osserviamo da sempre sui mercati, che importazioni ed esportazioni reagiscono al tasso di cambio, sono cioè “elastiche” al cambio. Del resto questo è esattamente il motivo per il quale gli alamanni hanno costruito un'Europa nella quale chi ha un surplus di 200 miliardi di dollari non possa rivalutare! Quello che succede alla fine della storia dipende appunto da quantosono elastiche esportazioni e importazioni. Da questo orecchio i materieprimisti non ci sentono, eppure non è poi così difficile strutturare un discorso serio.
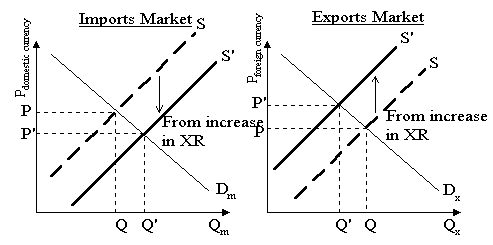
Il fatto è che quando il cambio si svaluta (E cresce) i prodotti nazionali diventano più convenienti (le esportazioni aumentano) e quelli esteri meno convenienti (le importazioni diminuiscono). Avremo quindi due elasticità delle esportazioni al cambio. Se la quotazione è incerto per certo, quella delle esportazioni sarà positiva, quella delle importazioni negativa.
(Nota: che se invece la quotazione fosse, come va di moda ora nell'Eurozona, certo per incerto, i segni sarebbero cambiati. In quel caso, infatti, una svalutazione si tradurrebbe in una diminuzione del cambio, e quindi l'elasticità delle esportazioni sarebbe negativa (se il cambio scende, le esportazioni salgono), e quella delle importazioni positiva. Sotto vediamo un esempio).
Questi effetti evidentemente contrastano l’effetto negativo determinato dalla svalutazione del cambio sul costo delle importazioni. L’aumento del costo delle importazioni fa peggiorare la situazione (è lo scenario materieprimista visto sopra), ma sia l’aumento del volume delle esportazioni che la riduzione di quello delle importazioni tendono a far migliorare la situazione.
Il problema è: quanto devono essere elastiche esportazioni e importazioni affinché il movimento dei loro volumi compensi l’effetto negativo dato dall’aumento del valore delle importazioni?
La regola è molto semplice e si chiama condizione di Marshall-Lerner: bisogna che la somma dei valori delle due elasticità, presi tutti col segno positivo (cioè in valore assoluto, come si dice in matematica) sia maggiore di uno. Ovviamente, dato che l’elasticità delle esportazioni è già positiva, prima di sommare le elasticità basta cambiare segno all’elasticità delle importazioni (ricordando sempre che se il cambio è quotato al contrario, le elasticità cambiano segno, ma non ce ne frega niente, perché tanto a noi interessa il loro valore assoluto).
Prima di darvi la doverosa dimostrazione (che comunque trovate su Internet in tutte le salse), vi fornisco qualche esempio, riprendendo la tabella precedente alla quale ho aggiunto tre colonne: una per l’elasticità al cambio delle esportazioni (exp), una per quella delle importazioni (imp), e una per la somma dei loro valori assoluti (ML).
Lo scenario del materieprimista, lo avrete capito, corrisponde al caso assolutamente improbabile in cui né esportazioni né importazioni variano, per cui la loro elasticità al cambio è nulla: zero per le esportazioni, zero per le importazioni, e quindi, siccome zero più zero uguale zero, la condizione di Marshall-Lerner non è rispettata: la somma delle elasticità (zero) è minore di uno.
Ma attenzione.
Non occorre essere ottusi come un materieprimista perché la condizione non venga rispettata.
Guardate ad esempio il caso (A). Faccio con voi i conti passo passo. Intanto, ho immaginato che le elasticità siano 0.4 per l’export e -0.4 per l’import. La somma dei valori assoluti è 0.8<1, quindi la condizione non è rispettata e già possiamo immaginare che le cose finiranno male.
Infatti nel caso (A) le esportazioni in volume aumentano, ma, dato che il cambio è aumentato del 20%, il loro incremento è solo di 0.2x0.4=0.08=8%, cioè le esportazioni passano da 50 a 54 (essendo 4 appunto l’8% di 50 per quella storia che cerco di far capire a Uga secondo la quale 5x8=40...). Dato che i prezzi rimangono fissi, anche il valore delle esportazioni passa da 50 a 54.
Quanto al volume delle importazioni, lui, certo, diminuisce, ma solo dello 0.2x(-0.4)=-8%. Ilvolume delle importazioni quindi scende a 46. Solo che siccome il cambio è aumentato del 20%, il valore delle importazioni è pari a 46x1.2=55.2, quindi aumenta rispetto alla baseline.
Certo, sono aumentate anche le esportazioni, ma solo fino a 54: il risultato quindi è che i conti passano in rosso per -1.2.
Bello, vero?
Dai, se ne fa un’altra...
Vediamo ad esempio il caso (B). Qui ho immaginato che le elasticità siano un po’ più grandi, del 60% per import e export, somma dei valori assoluti 1.2>1, quindi la condizione di ML è rispettata. Ci dobbiamo aspettare allora che una svalutazione migliori il saldo, portandolo in positivo, e in effetti è così, come verifichiamo insieme.
Dunque: le esportazioni in volume aumentano, questa volta del 0.2x0.6=0.12=12%, passando da 50 a 56 (che è appunto uguale a 50x1.12). Supponendo che i prezzi siano fissi, questo è anche l’aumento del valore delle esportazioni. Le esportazioni aumentano quindi più di prima, ma questo basta a sconfiggere l’incubo dei materieprimisti?
Vediamo: le importazioni, in volume, diminuiscono del 12%, passando a 44. Certo, il loro valore è influenzato dal fatto che il cambio è aumentato del 20%, e quindi corrisponde a 44x1.2=52.8. Caspita! Anche in questo caso il materieprimista ha ragione! Mi trovo a pagare le importazioni più di prima... Ma... Oooops! Non sto forse dimenticando qualcosa? Ah, già! È vero che pago le importazioni 2.8 lire in più che nella baseline, ma è anche vero che dalle esportazioni ricavo 6 lire in più. Quindi il mio saldo migliora di 3.2 lire.
Abbiamo sconfitto l’incubo del materieprimista!
Notate che il risultato funziona quando anche solo uno dei flussi (solo l’export, o solo l’import) è elastico, purché la somma delle elasticità sia maggiore di uno: lo vedete nei casi (C) e (D).
Dalla teoria alla pratica
Ma queste elasticità, in pratica, quanto valgono? Quanto è plausibile che siano così grandi da tirarci fuori dai guai?
Ovviamente il dibattito su questo punto sarà eterno, e se volete un giorno ve ne racconto la storia, che conosco piuttosto bene, a partire dal primo articolo rilevante, quello di Houthakker e Magee (1969) su American Economic Review. Qui mi limito a farvi osservare una cosa. Vi ricordate di quando abbiamo parlato del Verbum Domini? Sì, insomma, di quell’altra strana genia, i competitivitànondiprezzisti, un’altra categoria di fuuuuuuuuuuuurbi che confuta le strane teorie di Bagnai venendogli a spiegare (perché loro hanno lavorato, son stati in azienda e hanno fatto il militare a Corato) che quello che conta non sono i prezzi ma la qualità del prodotto, della rete di assistenza, ecc. (senza sapere che il povero Bagnai si è nutrito di pane eFagerberg lavorando per Pier Carlo Padoan, ma lasciamo perdere...). Bene. Lì vi ho citato un rapporto trimestrale della Commissione Europea il quale serenamente ammette che la competitività non di prezzo sarà anche importante in teoria, ma in pratica c’entra poco, perché il diverso comportamento delle esportazioni fra Italia e Germania è spiegato interamente dal comportamento del tasso di cambio reale (cioè corretto per l’inflazione).
È interessante vedere quali sono le elasticità delle esportazioni al cambio secondo gli esperti della commissione. Vi riporto il pezzo rilevante del loro Box IV.1:
Le elasticità al cambio sono nella colonna REER. Attenzione: REER significa real effective exchange rate, ed è appunto la misura del tasso di cambio sensata per una stima simile. Vi ricordo che il tasso di cambio reale è il rapporto fra il livello dei prezzi interni ed esteri espressi nella stessa valuta, e quindi nel nostro caso sarebbe:
(prezzi interni in valuta nazionale, diviso prezzi esteri in valuta nazionale). Notate che il cambio reale è sempre quotato certo per incerto, cioè in ogni caso una sua diminuzione corrisponde a una svalutazione reale, cioè a un aumento della convenienza dei beni interni, per qualsiasi motivo (perché diminuiscono i prezzi interni, perché si svaluta il cambio, perché aumentano i prezzi esteri).
Ora, caso vuole che se consideriamo i prezzi interni ed esteri come fissi, il cambio reale varia solo se cambia quello nominale, e sostanzialmente dello stesso importo: se E si svaluta (sale) del 20%, er si svaluta (scende) di circa lo stesso importo.
E qui arriva l’ennesimo fuuuuuuuuuuuuuuurbo, il circoloviziosista: “Bagnai vuole ingannarmi, ma a me non la si fa! Io sono fuuuuuuuuuuuurbo. Si sa, è noto che l’immorale svalutazione immediatamente genera inflazione e quindi se aumenta E, abbassando il cambio reale, poi aumenta P, riportandolo dov’era prima, ecc. ecc.”. Vabbe’, questo è solo un poro cojone, inutile perderci tempo: abbiamo visto in tutte le salse che la svalutazione non si traduce interamente in inflazione né nel breve né nel lungo periodo, e per chi non fosse convinto c’è tanto bella la Fig. 12 del mio libro. Nel breve-medio periodo è senz’altro lecito supporre che i prezzi non compensino le variazioni del cambio, che possono essere rapide ma si trasmettono con ritardi e solo in parte ai prezzi, dal che deriva che le elasticità al cambio reale di fatto ci dicono cosa succede se varia il cambio nominale.
E l’altra “E”, quella di “effective”?
Scusate, ma perché non lo chiedete a quel pirla secondo il quale io ormai dovevo chiudere il blog perché voi sapete già tutto? Ecco, cercatevi su Wikipedia (non quella italiana, la fiera della disinformazione) cos’è un cambio effettivo, e la prossima volta siate umili, che qua di superbo basto io.
Anyway, quanto sopra per dirvi che le elasticità della colonna REER possono essere prese come misura dell’impatto del cambio sulle esportazioni. Dice: ma perché sono negative? Dico: ma perché abbiamo visto che con le convenzioni che stiamo usando (e che sono quelle in uso fuori dall’Eurozona) la svalutazione nominale corrisponde a un aumento di E, ma quella reale a una diminuzione di er, e quindi il segno dell’elasticità cambia. Ma a noi non ce ne frega niente, perché quello che è rilevante comunque è la somma dei valori assoluti, capite?
Bene, guardiamo ‘sta tabella. Cosa vedete? Sono rispettate le condizioni di Marshall-Lerner?
Dice: ma ci mancano le elasticità al prezzo delle importazioni! Non possiamo fare la somma.
Ehi, amico, scusa, guarda bene: in Spagna, Francia e Italia le elasticità di prezzo delle esportazioni sono, già loro, maggiori di uno. Capisci, amico? Siamo nel caso (C) della tabella, quello in cui solo le esportazioni sono elastiche ai prezzi... Ma con una elasticità simile, maggiore di uno, se anche le importazioni in volume non si muovessero, l’aumento di costo determinato dalla necessità di pagare di più la valuta estera verrebbe più che compensato dall’aumento di ricavi prodotto dall’incremento del volume delle esportazioni. Quindi in tutti questi paesi (che guarda caso sono tutti del Sud, Francia inclusa) una uscita con svalutazione avrebbe necessariamente effetti positivi sul saldo commerciale.
E notate un altro fatto interessante. In quale paese le esportazioni sono più elastiche al prezzo? E quindi a quale paese converrebbe di più tirarsi fuori dl letamaio dell'euro?
L'I...
L'It....
L'Ita....
L'Ital...
L'Itali....
L'Italia....
"L'Italia!"
Sì. ecco, bravi, avete indovinato subito! Bene: ora dovete solo raccontarlo a una minoranza rumorosa di traditori degli interessi del proprio paese, e convincerli, e siamo a posto: ecco risolto il problema politico!
(Ah, ovviamente il trollazzo demente - Alex78 - era intervenuto su Verbum Domini per farmi capire che io avevo sbagliato, visto che avevo trascurato le importazioni, ma così mi ha fatto solo capire che non conosceva le condizioni di Marshall-Lerner... Porello... Con queste elasticità delle esportazioni - e si può discutere di quanto siano affidabili - di sapere cosa fanno le importazioni non ce ne fotte niente).
Intanto, la dimostrazione delle condizioni ve la fate per esercizio. Qui c’è l’esempio con il cambio quotato certo per incerto, potrete adattarlo voi al caso che studiamo qui (nota che l’elasticity pessimism di Wikipedia è datato e fuorviante, ma di questo si può parlare un’altra volta). Se siete tanto bravi da volere la dimostrazione, siete anche tanto bravi da capire perché ho scelto, per la prima parte di questo post, la quotazione incerto per certo (l’incubo del materieprimista... ricordate... quindi?).
(volete i post tecnici? E qui siamo solo all'inizio. Pensa quando parleremo di come scegliere le stime più rappresentative di queste benedette elasticità...)








Nessun commento:
Posta un commento